MECÁNICA 1: UNIDAD III. ESTUDIO DE ALGUNOS MOVIMIENTOS DE INTERÉS.

Tipos de movimientos:

MOVIMIENTO RECTILÍNEO UNIFORME

El movimiento rectilíneo uniforme (MRU) fue definido, por primera vez, por Galileo en los siguientes términos: "Por movimiento igual o uniforme entiendo aquél en el que los espacios recorridos por un móvil en tiempos iguales, tómense como se tomen, resultan iguales entre sí", o, dicho de otro modo, es un movimiento de velocidad v constante.

El MRU se caracteriza por:

a) Movimiento que se realiza en una sola dirección en el eje horizontal.

b) Velocidad constante; implica magnitud, sentido y dirección inalterables.

c) La magnitud de la velocidad recibe el nombre de rapidez. Este movimiento no presenta aceleración (aceleración = 0).

VIDEO DE MRU

GRÁFICAS DESPLAZAMIENTO-TIEMPO Y VELOCIDAD TIEMPO

Un cuerpo realiza un movimiento rectilíneo uniforme cuando su trayectoria es una línea recta y su velocidad es constante. En este apartado vamos a estudiar las gráficas del m.r.u, es decir:

Gráfica posición-tiempo (x-t)

x = x 0 + v \cdot t

La gráfica posición-tiempo (x-t) de un movimiento rectilíneo uniforme (m.r.u.). representa en el eje horizontal (eje x) el tiempo y en el eje vertical la posición. Observa como la posición (normalmente la coordenada x) aumenta (o disminuye) de manera uniforme con el paso del tiempo. Podemos distinguir dos casos, cuando la velocidad es positiva o negativa:

Gráfica posición - tiempo (x-t) en m.r.u.

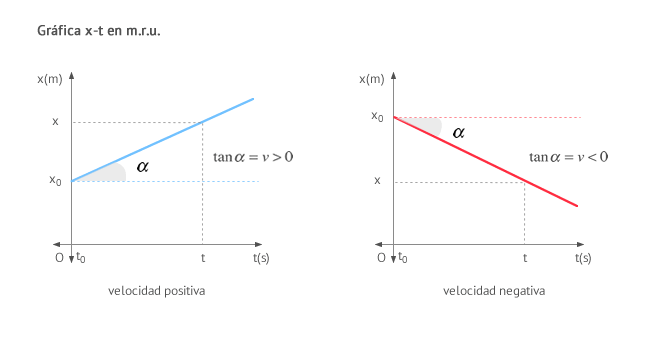
Gráfica velocidad-tiempo (v-t)

v = v 0 = cte

La gráfica velocidad-tiempo (v-t) de un movimiento rectilíneo uniforme (m.r.u.) muestra que la velocidad permanece constante a lo largo del tiempo. De nuevo, podemos distinguir dos casos:

Gráfica velocidad - tiempo (v-t) en m.r.u.

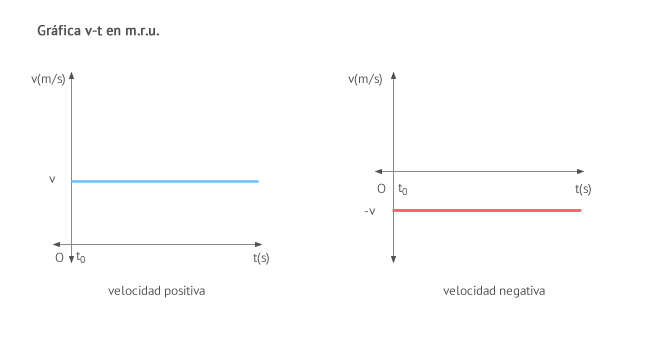
Observa que el área que limitada bajo la curva v entre dos instantes de tiempo es el espacio recorrido.

Espacio recorrido en m.r.u. a partir de la gráfica velocidad - tiempo (área bajo la curva)

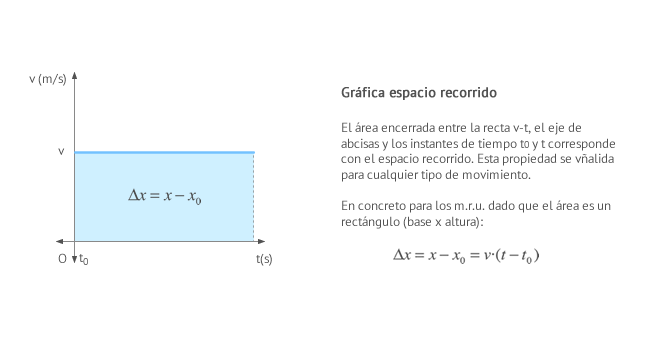
Gráfica aceleración-tiempo (a-t)

a = 0

La gráfica aceleración-tiempo (a-t) de un movimiento rectilíneo uniforme (m.r.u.) muestra que la aceleración es nula en todo momento. En este caso, tanto si la velocidad del cuerpo se considera positiva como negativa, tenemos una sola posibilidad, ilustrada en la figura:

Gráfica aceleración - tiempo (a-t) en m.r.u.

PRÁCTICA REAL DE MOVIMIENTO RECTILINEO UNIFORME

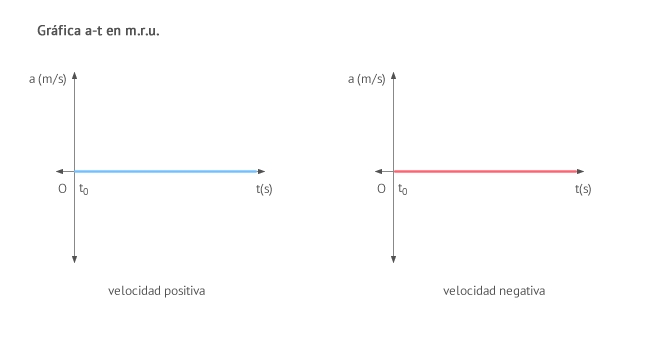
EL siguiente archivo, es el reporte de la práctica de movimiento rectilineo uniforme, bajalo e imprimelo para su uso en el desarrollo de la práctica de laboratorio:

http://www.4shared.com/file/2rRkLLtxba/PRACTICA_1__MRU.html

PAGINA VIRTUAL DE MRU

Las siguientes páginas muestras el desarrollo de MRU, en gráfica:

http://www.educaplus.org/play-125-MRU-Gráfica-e-t.html

http://www.educaplus.org/play-126-MRU-Gráfica-v-t.html

http://www.xtec.cat/~ocasella/applets/movrect/appletsol.htm

http://www.educaplus.org/play-300-Gráfica-v-t.html

http://www.educaplus.org/play-350-Movimiento-rectil%C3%ADneo-uniforme.html

P.D. Haga lo que puede, con lo que tenga, donde esté. (Theodore Roosevelt)

GRAFICA DESPLAZAMIENTO-TIEMPO MRU

GRÁFICA VELOCIDAD-TIEMPO MRU

VÍDEO DE PROBLEMAS RESUELTOS MRU

Modelos matemáticos MRU

V= d/t

d = V. t

Donde:

d = d_f - d_o

t = t_f - t_o

P.D. El mayor descubrimiento de cualquier generación es el que los seres humanos pueden cambiar sus vidas cambiando sus actitudes. Albert Schweitzer

AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA

MOVIMIENTO RECTILÍNEO UNIFORMEMENTE

ACELERADO

El movimiento rectilíneo uniformemente acelerado (m.r.u.a.), también conocido como movimiento rectilíneo uniformemente variado (m.r.u.v), es un movimiento rectilíneo con aceleración constante, y distinta de cero. En este apartado vamos a estudiar:

Gráficas de M.R.U.A.

Gráfica posición-tiempo (x-t)

x = x 0 + v 0 t + 1 2 a t 2

La gráfica posición-tiempo (x-t) de un movimiento rectilíneo uniformemente acelerado (m.r.u.a.) o movimiento rectilíneo uniformemente variado (m.r.u.v.) representa en el eje horizontal (eje x) el tiempo y en el eje vertical (eje y) la posición. Observa como la posición (normalmente la coordenada x) aumenta (o disminuye) de manera no uniforme con el paso del tiempo. Esto se debe a que, a medida que este pasa, el módulo de la velocidad varía. Podemos distinguir dos casos, cuando la aceleración es positiva o negativa:

Gráfica posición - tiempo (x-t) en m.r.u.a.

Gráfica velocidad-tiempo (v-t)

v = v 0 + a \cdot t

La gráfica velocidad-tiempo (v-t) de un movimiento rectilíneo uniformemente acelerado (m.r.u.a.) o movimiento rectilíneo uniformemente variado (m.r.u.v.) representa en el eje horizontal (eje x) el tiempo y en el eje vertical (eje y) la velocidad. Observa como la velocidad aumenta (o disminuye) de manera uniforme con el paso del tiempo. Esto se debe a la acción de la aceleración. De nuevo, podemos distinguir dos casos:

Gráfica velocidad- tiempo (v-t) en m.r.u.a.

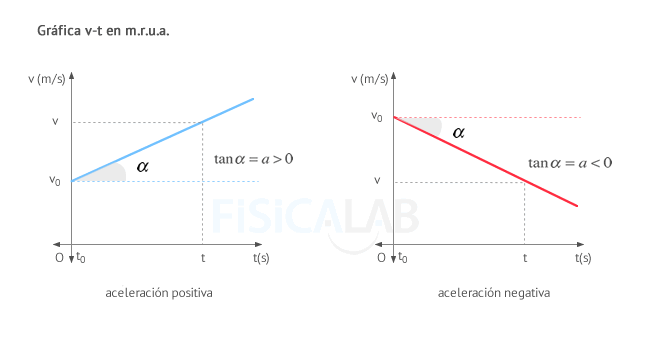
A partir del ángulo α puedes obtener la aceleración. Recuerda para ello que, en un triángulo rectángulo se define la tangente de uno de sus ángulos como el cateto opuesto partido la hipotenusa:

tan α = cateto opuesto cateto contiguo = ∆ v ∆ t = v - v 0 t = a

El valor de la pendiente es la propia aceleración. Por tanto a mayor pendiente de la recta, mayor aceleración posee el cuerpo.

Observa que el área limitada bajo la curva v entre dos instantes de tiempo coincide numéricamente con elespacio recorrido. ¿Sabrías decir por qué?

Espacio recorrido y área bajo la gráfica de velocidad en m.r.u.a.

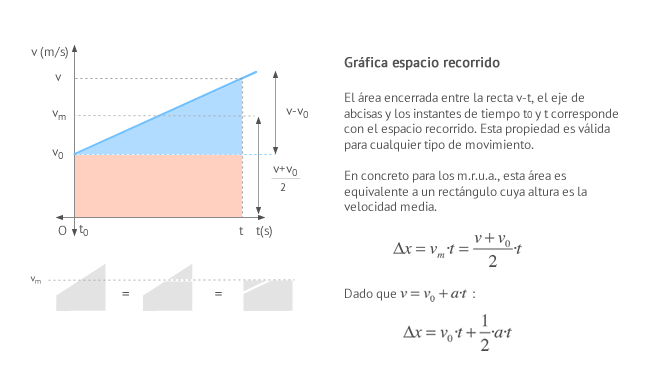
El área bajo la curva puede calcularse como el aréa del rectángulo S1 que correspondería a un movimiento rectilíneo uniforme (m.r.u) a la que sumaremos el área del triángulo S2:

∆ x = x - x 0 = S 1 + S 2 =    1 v 0 t + ( v - v 0 ) t 2 =    2 v 0 t + 1 2 a t 2

Donde hemos aplicado:

{S1=v0tS2=Srectángulo2=(v−v0)t2
v−v0=at

Gráfica aceleración-tiempo (a-t)

a = cte

La gráfica aceleración-tiempo (a-t) de un movimiento rectilíneo uniformemente acelerado (m.r.u.a.) o movimiento rectilíneo uniformemente variado (m.r.u.v.) muestra que la aceleración permanece constante a lo largo del tiempo. Se trata de la aceleración media, que en el caso de m.r.u.a., coincide con la aceleración instantánea. De nuevo, podemos distinguir dos casos:

Gráfica aceleración - tiempo (a-t) en m.r.u.a.

Observa que el área limitada bajo la curva a entre dos instantes de tiempo coincide numéricamente con el incremento de velocidad experimentado. ¿Sabrías decir por qué?

PAGINA VIRTUAL DE MRUA

Las siguientes páginas muestras el desarrollo de MRU, en gráfica:

http://www.educaplus.org/play-238-Graficas-del-movimiento.html?PHPSESSID=215d27f70db8987b6b49e5a4f4bade8a

http://www.educaplus.org/play-123-MRUA-Gráfica-e-t.html

http://www.educaplus.org/play-124-MRUA-Gráfica-v-t.html

http://www.walter-fendt.de/ph14s/acceleration_s.htm

GRAFICA VELOCIDAD-TIEMPO MRUA

VÍDEO EJEMPLO DE MRUA

Modelos matemáticos MRUA
V_f = V_o + a.t

V_f² = V_o² + 2a.d

d = V_o . t + ½ a. t²

d =(V_o +V_f).t /2

P.D. Procure no ser un hombre con éxito, sino un hombre con valores. (Albert Einstein)

P.D. El único sitio donde el éxito llega antes que el trabajo es en el diccionario. (Vidal Sassoon)

CCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCC

CAÍDA LIBRE

La caída libre es un caso particular del movimiento rectilíneo uniformemente acelerado, es cuando un cuerpo se le deja caer libremente en la cercanía de la superficie del planeta.

Un cuerpo que se deja caer en el vacío, se desplaza en linea recta vertical con una aceleración constante, la cual se conoce como gravedad (g), lo que produce que el módulo de la velocidad aumente uniformemente en el transcurso de su caída.

PAGINA VIRTUAL DE CAÍDA LIBRE

Las siguientes páginas muestras el desarrollo de caída libre, en gráfica:

http://www.educaplus.org/play-301-Caída-libre.html

http://www.educaplus.org/play-302-Gráficas-de-la-caída-libre.html

Video de caida libre:

http://www.youtube.com/watch?v=s5QcJfMH-es&feature=related
http://www.youtube.com/watch?v=xGErI2_Xc1c&feature=related

Modelos matemáticos caída libre

V_f = g.t g = -9.81 m/seg²

V_f² = 2g.h
h = ½ g. t²

h =(V_f. t)/2

LLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLL

PAGINA VIRTUAL DE LANZAMIENTO VERTICAL

Las siguientes páginas muestras el desarrollo de lanzamiento vertical, en gráfica:http://www.xtec.cat/~ocasella/applets/caiguda/appletsol.htm

TIRO VERTICAL

La noción de tiro vertical aparece en el campo de la física. Se trata de un movimiento rectilíneo uniforme variado, también conocido como MRUV. En un tiro vertical, la velocidad cambia y existe una aceleración que está dada por la acción de la gravedad.

El tiro vertical, cuya dirección puede ser descendente o ascendente, tiene una velocidad inicial que resulta diferente a cero. El cuerpo en cuestión se lanza hacia arriba, impulsado con una cierta velocidad. Luego regresa al punto de partida con la misma velocidad, aunque en un sentido contrario a la que tenía en el momento del lanzamiento.

Puede decirse, de este modo, que el cuerpo lanzado en un tiro vertical sube y luego baja, regresando al punto de partida. Cuando el cuerpo alcanzó la altura máxima, la velocidad resulta nula. En ese instante, el cuerpo deja de subir e inicia su descenso. El tiempo que el cuerpo demora en llegar a la altura máxima resulta idéntico al tiempo que tarda en volver a su punto de partida.

Es importante destacar que existen diversas ecuaciones que permiten medir diferentes magnitudes vinculadas al tiro vertical. Estas ecuaciones trabajan con variables como la velocidad inicial, la altura y la aceleración.

https://youtu.be/7ubmjc5xKCs

https://youtu.be/YAUDlm4BCME

Modelos matemáticos tiro vertical

V_f = V_o+ g.t g = -9.81 m/seg²

V_f² = V_o²+ 2g.h

d = V_o . t + ½ g. t²

d =( V_o +V_f).t /2

P.D.Para triunfar en la vida, no es importante llegar el primero. Para triunfar simplemente hay que llegar, levantándose cada vez que se cae en el camino.

PPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPP

TIRO PARABÓLICO

Se denomina movimiento parabólico al realizado por cualquier objeto cuya trayectoria describe una parábola. Se corresponde con la trayectoria ideal de un proyectil que se mueve en un medio que no ofrece resistencia al avance y que está sujeto a un campo gravitatorio uniforme. El movimiento parabólico es un ejemplo de un movimiento realizado por un objeto en dos dimensiones o sobre un plano. Puede considerarse como la combinación de dos movimientos que son un movimiento horizontal uniforme y un movimiento vertical rectilíneo.

FOLLETO

http://www.4shared.com/file/FeiLSwDy/folleto_tiro_parabolico.html

VIDEO TIRO PARABOLICO

TIRO HORIZONTAL

P.D.Para empezar un gran proyecto, hace falta valentía. Para terminar un gran proyecto, hace falta perseverancia.

TIRO OBLICUO

DIRECCIÓN DE LA PRÁCTICA VIRTUAL TIRO PARABOLICO

Las siguientes direcciones de la web, son los applets vistos en el laboratorio de física, entrar en ellas para manipularlas y entregar reporte la siguiente sesión de clases:http://www.educaplus.org/play-109-Tiro-horizontal.html
http://www.educaplus.org/play-110-Tiro-parabólico.html
http://www.educaplus.org/play-305-Alcance-y-altura-máxima.html
http://www.educaplus.org/play-308-Cañones-complementarios.html
http://www.educaplus.org/play-303-Gráficas-del-lanzamiento-horizontal.html
http://www.educaplus.org/play-304-Principio-de-Independencia.html

PD.Todo tiene algo de belleza pero no todos son capaces de verlo (Confucio)

Modelos matemáticos tiro parabolico

Movimiento horizontal (MRU)

d = V. t

Movimiento vertical (MRUA)

V_f = V_o+ g.t g = -9.81 m/seg²

V_f² = V_o²+ 2g.h

h = V_o . t + ½ g. t²

h =( V_o +V_f).t /2

P.D. El Gran Arquitecto del Universo hizo al hombre con dos orejas y una boca; para que escuche el doble de lo que habla. Autor: Proverbio Chino